什么是锂离子动力学？

 

(1)锂离子在LiCoO _{2中的扩散系数}

以球形电极模型处理锂离子在多孔LiCoO ₂ 电极中的扩散为例，假设：

① LiCoO ₂ 电极中每个活性物质颗粒均采用球形电极处理；

②电极过程由一个恒电位步骤控制，步骤电位很高，所以步骤后电极表面的锂离子浓度可以设置为0；

_{③由于锂离子在LiCoO 2}电极固相中的扩散速率 远低于液相，整个电极过程受锂离子在固相中的扩散速率控制；

④ 以球心为坐标原点，半径为r的球面上各点的径向流为：

r=r+dr 球面上各点的径向流量为：

式中，c为LiCoO2固相中半径r处锂离子的浓度；D _Li+ 为锂离子在LiCoO2颗粒中的扩散系数，如图1和图2所示。

_{图 1 - LiCoO 2} 颗粒被球形处理的电极示意图

图2——球形扩散示意图

在两个球体之间的极薄球壳中，反应粒子浓度的变化率为：

结合以上三个公式，可以得到菲克第二定律在球坐标系中的表达式：

初始条件：当t=0, 0<r<r ₀ , c(r,0)=c ₀

式中，r _0为LiCoO 2粒子 的半径 ；c ₀是 工序开始前的LiCoO ₂粒子 中的锂离子浓度。

边界条件：当t>0时，r=r ₀ , c(r ₀ , t)=0；当 0<t<τ, r=0, c(r,0)=c ₀。

 式中，τ为扩散后扩散层边界延伸至LiCoO ₂颗粒中心的时间。

在上述初始和边界条件下，求解方程 ，得到LiCoO ₂电极 中锂离子浓度的表达式 ：

将上式对r微分得到：

将r=r ₀代 入上式，可得：

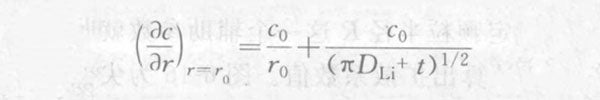
由此，求解潜在步骤后的当前响应：

式中，n为获得或失去的电子数；F是法拉第常数；A是电极面积。

^{上式表明，测试工作电极的电流I与t -1/2}之间存在线性关系。 利用这一特征，可以计算出LiCoO ₂颗粒中锂离子的扩散系数。将上式改写为 I=B+Kt ^-1/2。

其中，  .

锂离子扩散系数D _Li+ 可以由B和K两个公式求得：

(2)锂离子在LiMn ₂ O _{4中的扩散系数}

根据球形扩散模型，恒压恒流充电容量比值可表示为：

式中，ξ= R ² / D ^t，无量纲；R为粒子半径，cm；t为恒流充电时间，s；D为固相扩散系数，cm ² /s；α _j 是常数序列，由方程tanα=α have to 求解。将上述方程在不同q值范围内用最小二乘法对ξ进行线性拟合，最终得到一系列方程D=f(q)，如表1所示。根据表1，只要测量粒子半径R、恒压恒流充电容量比q和恒流充电时间t，即可得到扩散系数D。

表 1 - 不同 q 值范围内最小二乘法线性拟合方程

图 3 在第一个循环中测量的体积间隙滴定 (CITT) 曲线。t值可以从图3(a)的电压-时间或电流-时间曲线得到，q值可以从图3(b)的电压-容量曲线得到。因此，从CITT曲线得到的数据可以通过测量粒子半径R作为辅助参数得到，扩散系数值可以从表1中的公式计算得到。图4显示了测量的前20个循环的CITT曲线采用尖晶石LiMn ₂ O ₄ /Li电池，稳定性好。根据图4，锂离子在LiMn ₂ O _{4中的扩散系数前20次充放电过程的计算结果如图5所示。从图5可以看出，锂离子在LiMn 2} O ₄ 中的固相扩散系数不仅与电压有关，也与锂的浓度有关 。 Mn ₂ O ₄ 晶格中的离子或电荷深度 (DOC)，而且扩散系数在充电循环期间发生显着变化。. 随着电压的变化，在3.95V和4.12V附近出现两个极小的峰值，整个扩散系数电压曲线呈扭曲的“W”形。

 图3-恒流充电电流下测得的尖晶石LiMn ₂ O _{4的第一条CITT曲线}

_{图 4 - 尖晶石 LiMn 2} O ₄的前 20 条 CITT 曲线

_{图5 - LiMn 2} O ₄中锂离子的前20 lgD-E曲线

采用容积间歇滴定技术可以方便地检测出不同电压、不同充放电循环次数下嵌入离子在电极材料中的扩散系数。

(3)锂离子在石墨中的扩散系数

在电势阶跃区间内，假设锂离子扩散系数不随其在电极材料中的浓度而变化，电势阶跃后，锂离子在球形电极材料中的扩散符合菲克第二定律。经过推导，可以得到响应电流i与时间t的关系：

该公式的适用条件是t<R ² /D。其中 i(t) 是电位阶跃后的响应电流；S为球形颗粒的表面积；F是法拉第常数；D为锂离子扩散系数；c ₀ 和c _a 为电位阶跃前后的锂离子浓度；R是粒子半径。根据上式，响应电流i(t)与t ^-1 / 2 在短时间内满足线性关系。从这个关系，可以获得锂离子扩散系数。

假设石墨材料的摩尔体积为V _m，它不随锂离子浓度的变化而变化。1摩尔物质的表面积与体积的关系为 

. 通过步长间隔的电量ΔQ(mA·h)与锂离子浓度变化的关系为ΔQ=0.2778 n _c F V _m ( c _a - c ₀ )，n _c 为石墨量在极片中。设m(mA·s ^{1 / 2 )为响应电流i与t -1/2}线性关系的斜率。推导后，半径为R(cm)的石墨负极材料中锂离子扩散系数的计算表达式为：

事实上，石墨材料颗粒的形状多种多样，即使是石墨化中间相碳颗粒（MCMB）也不会有完美的球形。考虑到颗粒的实际形状，一般采用BET法测得的比表面积来计算锂离子扩散系数。

通过电化学方法计算材料的真实比表面积S，并计算锂离子扩散系数，可以获得更可靠的值。推导的锂离子扩散系数与实际比表面积S _e  (cm ² /g)和密度ρ (g/cm ³ )的关系为：